commit
995ede2350
7 changed files with 822 additions and 0 deletions
Unified View
Diff Options
-
BINDiff-Circle.avi
-
+81 -0Readme.md
-
+741 -0ficks.ipynb
-
BINoutput_2_0.png
-
BINoutput_5_0.png
-
BINoutput_5_48.png
-
BINoutput_5_7.png
BIN
Diff-Circle.avi
View File
+ 81
- 0
Readme.md
View File
| @ -0,0 +1,81 @@ | |||||
| ```python | |||||
| from fenics import * | |||||
| from dolfin import * | |||||
| import mshr | |||||
| import matplotlib.pyplot as plt | |||||
| import numpy as np | |||||
| ``` | |||||
| ```python | |||||
| T = 60*60*5 #final step | |||||
| num_steps = 50 | |||||
| dt = T/num_steps #step size | |||||
| ``` | |||||
| ```python | |||||
| #2 Create mesh and define function space | |||||
| domain = mshr.Circle(Point(0.,0.),1.0,60) | |||||
| mesh = mshr.generate_mesh(domain, 25) | |||||
| V = FunctionSpace(mesh, 'Lagrange', 1) #Lagrange are triangular elements | |||||
| plot(mesh) | |||||
| plt.show() | |||||
| ``` | |||||
|  | |||||
| ```python | |||||
| #3 Defining boundary conditions (Dirichlet) | |||||
| D = 1.4E-7 #cm^2/s | |||||
| u_D = Constant(0.1) | |||||
| def Dirichlet_boundary(x, on_boundary): | |||||
| return on_boundary | |||||
| bc = DirichletBC(V, Constant(1), Dirichlet_boundary) | |||||
| ``` | |||||
| ```python | |||||
| #Defining initial values and variational problem | |||||
| u_n = interpolate(u_D,V) | |||||
| u = TrialFunction(V) | |||||
| v = TestFunction(V) | |||||
| f = Constant(0) | |||||
| F = u*v*dx+D*dt*dot(grad(u), grad(v))*dx-(u_n+dt*f)*v*dx | |||||
| a, L = lhs(F), rhs(F) | |||||
| ``` | |||||
| ```python | |||||
| #Resolution on time steps | |||||
| u = Function(V) | |||||
| t = 0 | |||||
| vtkfile = File('sol/solution.pvd') | |||||
| for n in range(num_steps): | |||||
| #update current time | |||||
| t += dt | |||||
| u_D.t = t | |||||
| #compute solution | |||||
| solve(a==L, u, bc) | |||||
| #vtkfile << (u,t) | |||||
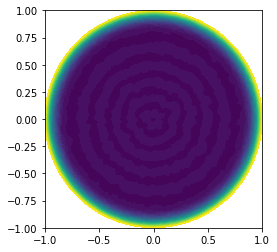
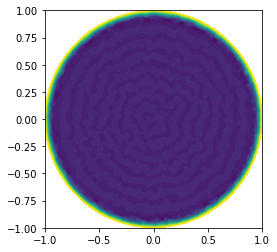
| plot(u) | |||||
| plt.show() | |||||
| #update previous solution | |||||
| u_n.assign(u) | |||||
| ``` | |||||
|  | |||||
|  | |||||